👉DISTRIBUCIÓN EXPONENCIAL: En una gran parte de los modelos continuos relacionados con el tiempo podemos notar que su distribución es de tal forma que en los tiempos cercanos a cero tiene una mayor acumulación y que conforme pasa el tiempo ésta decrece rápidamente de forma similar a una función exponencial negativa. Por ejemplo, en los modelos relacionados con las lineas de espera es común que en los primeros instantes el cliente tenga una mayor probabilidad de ser atendido que después de un tiempo transcurrido.
👉 Problema 03: 😆
En una tienda departamental el tiempo promedio de espera para ser atendido en cajas al pagar la mercancía es de 7 minutos. Determine la probabilidad de que: a) Un cliente espere menos de 4 minutos. b) Un cliente espere más de 9 minutos.
👉 Problema 04: 😆
La vida media de un televisor “s” es de 7 años. si esta vida puede considerarse como una variable aleatoria distribuida en forma exponencial,
a) ¿Cuál es la probabilidad de que un televisor de este tipo falle después del 7°-año de uso?
b) si se toma una muestra aleatoria de estos 10 televisores “S”, ¿Cuál es la probabilidad de que un televisor de esta muestra dure más de 12 años?
👉 Problema 06: 😆
El periodo de vida en años de una estufa de cierta marca tiene una distribución exponencial con un promedio de falla de μ=6 años. a) Cuál es la probabilidad de que una estufa falle después del 4 año? b) Cuál debe ser el tiempo de garantía que deberá tener la estufa si se desea que a lo más el 20 % de las estufas fallen antes de que expire su garantía?
👉 Problema 07: 😆
El periodo de vida en años de un interruptor eléctrico tiene una distribución exponencial con un promedio de falla de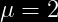 años ¿Cuál es la probabilidad de que un interruptor falle después del 2do año?
años ¿Cuál es la probabilidad de que un interruptor falle después del 2do año?
👉 Problema 08: 😆
Los administradores de cierta industria han notado que su producto tiene un tiempo de duración que puede considerarse una variable aleatoria con distribución exponencial con una vida media de 5 años. a)¿cuál es la probabilidad de que al elegir un artículo de dicha producción dure más de 10 años? b)¿si el tiempo de garantía asignado por los administradores es de 1 año, qué porcentaje de sus productos tendrá que reparar la industria durante el periodo de garantía?
👉 Problema 09: 😆
Una lavadora MABE tiene una vida media de 10 años. Si la vida útil de ese motor puede considerarse como una variable aleatoria distribuida en forma exponencial. ¿Cuál debe ser el tiempo de garantía que deben tener dichas lavadoras si desea que a los más 20 % de estas fallen antes de que expire su garantía?
👉 Problema 10: 😆
Un motor eléctrico tiene una vida media de 6 años. Si la vida útil de este tipo de motor puede considerarse como una variable aleatoria distribuida en forma exponencial. ¿Cuál debe ser el tiempo de garantía que debe tener el motor si se desea que a lo más el 15 % de los motores fallen antes de que expire su garantía?.
👉 Problema 11: 😆
El tiempo en que una computadora comercial permanece actualizada, se distribuye exponencialmente con una valor promedio de 2 años. ¿Cuál es la probabilidad de que una computadora comercial que se compra el día de hoy, permanezca actualizada dentro de 3 años?
👉 Problema 12: 😆
El tiempo de vida de un reo en cárceles de México a partir de su ingreso a algún reclusorio, se distribuye exponencialmente con un valor promedio 9 años. ¿Encuentre la probabilidad de que un reo que ingreso al reclusorio norte del D, F hace 15 años, siga con vida?
Ejemplo de distribución exponencial
Función de modelo exponencial
Sea 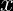 una variable aleatoria continua del experimento realizado,diremos que tiene una distribución exponencial con parámetro positivo
una variable aleatoria continua del experimento realizado,diremos que tiene una distribución exponencial con parámetro positivo 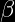 en el intervalo
en el intervalo ) , cuando su función de densidad de probabilidad es:
, cuando su función de densidad de probabilidad es:
Fácilmente se comprueba que la función anterior es efectivamente una función de densidad de probabilidad,puesto que no es negativa y la integral en todos los reales vale 1.
FUNCIÓN DE DENSIDAD
ESPERANZA MATEMÁTICA LLAMADO TAMBIÉN VALOR ESPERADO
DESVIACIÓN ESTÁNDAR LLAMADO TAMBIÉN VARIANZA
FUNCIÓN DE DISTRIBUCIÓN
FUNCIÓN DE SUPERVIVENCIA(COMPLEMENTO DE LA FUNCIÓN DE DISTRIBUCIÓN)
DISTRIBUCIÓN EXPONENCIAL EN LA VIDA COTIDIANA
😁Aplicación de los Modelos exponenciales:
Los modelos exponenciales tienen una gran aplicación en las lineas de espera o teoría de colas,por que las distribuciones de los tiempos son propicias para casos de:
1-Espera y llegada de clientes a un centro comercial.
2-Espera para reparar un aparato.
3-Espera para ser atendidos en un banco.
4-Espera para ser atendidos los pacientes en una clínica.
5-En algunos otros casos en los que se estudian las duraciones de vida de componentes electrónicos;
resulta que generalmente tienen una distribución tipo exponencial.
6-Duración de equipos industriales para poder establecer tiempos de garantías.
Con base en la relación anterior, entre los modelos de Poisson y Exponencial, con frecuencia muchas literaturas se emplea para los modelos exponenciales.
EJERCICIOS RESUELTOS
👉 Problema 01: 😆
Un componente eléctrico tiene una vida media de 8 años. Si su vida útil se distribuye en forma exponencial.
a)Cuál debe ser el tiempo de garantía que se debe otorgar, si se desea reemplazar a lo más el 15 % de los componentes que fallen dentro de este periodo?
Solución Inciso a)
Sea T el tiempo de garantía del componente eléctrico es necesario que:
eléctrico dure menos que el tiempo de garantía.
Extraemos logaritmo natural a ambos miembros
Finalmente
👉 Problema 02: 😆
El tiempo que tarda un empleado en tomar un pedido de un cliente en un restaurante que da servicio en su coche, sigue una distribución exponencial con una respuesta de atención al cliente de 4 minutos en promedio.
a)¿Que probabilidad hay de que el cliente siguiente deba esperar menos de 2.5 minutos?
b)¿Que probabilidad hay de que el cliente siguiente deba esperar entre 1 y 3 minutos?
Solución Inciso a)
La distribución exponencial tiene por
Formula
Solución Inciso b)
👉 Problema 03: 😆
En una tienda departamental el tiempo promedio de espera para ser atendido en cajas al pagar la mercancía es de 7 minutos. Determine la probabilidad de que: a) Un cliente espere menos de 4 minutos. b) Un cliente espere más de 9 minutos.
Solución Inciso a)
La distribución exponencial tiene por
Formula
Sacando el porcentaje:
Solución Inciso b)
La distribución exponencial tiene por formula,
La vida media de un televisor “s” es de 7 años. si esta vida puede considerarse como una variable aleatoria distribuida en forma exponencial,
a) ¿Cuál es la probabilidad de que un televisor de este tipo falle después del 7°-año de uso?
b) si se toma una muestra aleatoria de estos 10 televisores “S”, ¿Cuál es la probabilidad de que un televisor de esta muestra dure más de 12 años?
Solución Inciso a)
La distribución exponencial tiene por
Formula
Solución Inciso b)
Ahora usamos la formula de la binomial con parámetros:
La formula de la binomial es:
👉 Problema 05: 😆
El periodo de vida en años de un interruptor eléctrico tiene una distribución exponencial con un promedio de falla 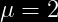 años.
años.
a) ¿Cual es la probabilidad de que al menos 8 de 10 de tales interruptores,que funcionan independientemente,fallen después del 3er año?
Solución Inciso a)
La distribución exponencial tiene por
Formula
Solución Inciso b)
Es decir que la probabilidad que un interruptor falle es 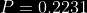 para calcular la probabilidad que al menos 8 de 10 fallen después del 3er año, necesitamos la distribución binomial con parámetros.
para calcular la probabilidad que al menos 8 de 10 fallen después del 3er año, necesitamos la distribución binomial con parámetros.
Ahora usamos la formula de la binomial con parámetros.
La formula de la binomial es:
👉 Problema 06: 😆
El periodo de vida en años de una estufa de cierta marca tiene una distribución exponencial con un promedio de falla de μ=6 años. a) Cuál es la probabilidad de que una estufa falle después del 4 año? b) Cuál debe ser el tiempo de garantía que deberá tener la estufa si se desea que a lo más el 20 % de las estufas fallen antes de que expire su garantía?
Solución Inciso a)
La distribución exponencial tiene por
Formula
Solución Inciso b)
Sea T el tiempo de garantía de las estufas, por otro lado, para que una estufa no falle antes de su tiempo de garantía, es necesario que:
que la estufa dure menos que el tiempo de garantía.
Extraemos logaritmo natural a ambos miembros
Finalmente
El periodo de vida en años de un interruptor eléctrico tiene una distribución exponencial con un promedio de falla de
Solución Inciso a)
La distribución exponencial tiene por
Formula
Los administradores de cierta industria han notado que su producto tiene un tiempo de duración que puede considerarse una variable aleatoria con distribución exponencial con una vida media de 5 años. a)¿cuál es la probabilidad de que al elegir un artículo de dicha producción dure más de 10 años? b)¿si el tiempo de garantía asignado por los administradores es de 1 año, qué porcentaje de sus productos tendrá que reparar la industria durante el periodo de garantía?
Solución Inciso a)
La distribución exponencial tiene por
Formula
Solución Inciso b)
Si el tiempo de garantía asignado por los administradores es de 1 año.
Formula:
Sacando el porcentaje del periodo de garantía:
👉 Problema 09: 😆
Una lavadora MABE tiene una vida media de 10 años. Si la vida útil de ese motor puede considerarse como una variable aleatoria distribuida en forma exponencial. ¿Cuál debe ser el tiempo de garantía que deben tener dichas lavadoras si desea que a los más 20 % de estas fallen antes de que expire su garantía?
Solución Inciso a)
Sea T el tiempo de garantía de las lavadoras, por otro lado, para que una lavadora sea reparada durante su tiempo de garantía, es necesario que:
que la lavadora dure menos que el tiempo de garantía,
Extraemos logaritmo natural a ambos miembros
Finalmente
Un motor eléctrico tiene una vida media de 6 años. Si la vida útil de este tipo de motor puede considerarse como una variable aleatoria distribuida en forma exponencial. ¿Cuál debe ser el tiempo de garantía que debe tener el motor si se desea que a lo más el 15 % de los motores fallen antes de que expire su garantía?.
Solución Inciso a)
Sea T el tiempo de garantía de los motores eléctricos,por otro lado, para que un motor eléctrico sea reparado durante su tiempo de garantia, es necesario que:
que el motor eléctrico dure menos que el tiempo de garantía
Extraemos logaritmo natural a ambos miembros
Finalmente
👉 Problema 11: 😆
El tiempo en que una computadora comercial permanece actualizada, se distribuye exponencialmente con una valor promedio de 2 años. ¿Cuál es la probabilidad de que una computadora comercial que se compra el día de hoy, permanezca actualizada dentro de 3 años?
Solución Inciso a)
La distribución exponencial tiene por
Formula
El tiempo de vida de un reo en cárceles de México a partir de su ingreso a algún reclusorio, se distribuye exponencialmente con un valor promedio 9 años. ¿Encuentre la probabilidad de que un reo que ingreso al reclusorio norte del D, F hace 15 años, siga con vida?
Solución Inciso a)
La distribución exponencial tiene por
Formula